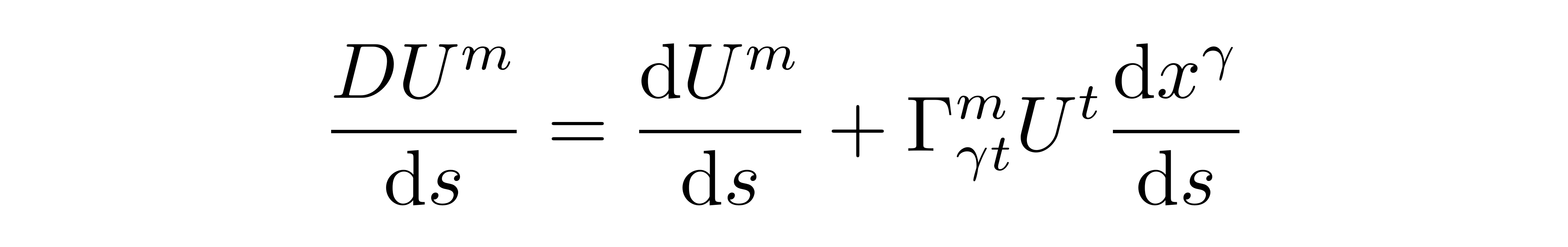betting line college football

这是由于，决定引力作用大小的“荷”恰好也是质量，将它和牛顿第二定律放在一起，质量恰好能从等号两边约去。这一事实在现在被命名为“弱等效原理”，它启发了爱因斯坦开始思考：为何引力的作用会如此普适，甚至不区分粒子？消去力的“荷”后，加速度究竟是怎样产生的？爱因斯坦的答案是：引力不是一种“力”，而是时空的弯曲，物体的加速度其实是几何效应。既然所有物体都得存在于时空上，那么也不难理解为何引力如此普适。

张朝阳介绍，这一认知促使爱因斯坦提出了广义相对论，广义相对论的基本思想即是大质量物体会造成时空的弯曲，从而影响了物体的运动轨迹。他自称，广义相对论在物理概念和数学形式上都相当有挑战，自己学习广义相对论就像登雪山一样。和登雪山要一段一段走过好几个营地一样，学习广义相对论也应该有若干个节点，首先是了解怎么描述一个弯曲的时空。这一步必要用到我们称之为张量的数学工具，具体的概念和定义已经在前两节直播课上介绍过。其中最重要的是被称为度规的二阶张量

被认为是刻画了时空性质的物理量。考察时空的弯曲，必然要涉及考察物理量的变化，所以还要涉及对张量的导数。为了让求导之后的结果同样构成张量，需要引入对普通偏导数的修正，从而构成协变导数（covariant derivative）

修正项由一个称之为克氏符的量决定，通过约定相容性条件

和无挠条件

可以推出克氏符完全由度规决定

由克氏符可以进一步构造出描述弯曲程度的几何量——曲率（curvature），这将是之后要着重介绍的内容。

张朝阳提醒，在讨论对弯曲的描述时，隐式地假设了存在一个给定地度规 g，再基于它去构造各种几何量。所以，理解了如何描述时空弯曲后，下一步要分析如何确定一个恰当地度规。事实上，确定度规形式的是爱因斯坦提出的广义相对论场方程。方程中，等号的左侧是几何的曲率，等号的右侧是描述引力源——比如一个大质量天体——性质的二阶张量，也称为能动张量。给定引力源，可以从场方程中反解出度规，再具体定下克氏符等几何量。

在这两个“营地”之间，其实还有一个重要的节点，即要问：在大质量物体的影响下，一个测试粒子是如何运动的？既然，引力不是一种通常意义上的“力”，而是时空的弯曲。那么当测试粒子仅受引力作用时，以弯曲时空上的观点，它其实是不受力的。牛顿第一定律提出，不受力的物体保持匀速直线运动。自然地可以期望，能不能将平直时空中的直线的概念，类比推广到在弯曲时空中。张朝阳介绍，这一类比即是弯曲时空中的“测地线”（geodesic）。平直时空中，不受力物体的运动轨迹是直线，而在弯曲时空中，不受力物体则将沿着测地线运动。

（张朝阳回顾张量和协变导数的定义）

测地线是弯曲时空上的“直线”

在球面上——比如地球上——的测地线就是一个大圆。走测地线的好处在于，连接两点之间的各种路径中，测地线的长度取到极值（极小或者极大），正如直线之于平直空间。张朝阳以从北京飞往纽约的航班为例，飞机的飞行路线会选择走过北极上空，经过安卡拉其、阿拉斯加……这条路径即是大圆的一部分，是两个城市之间的最短路径。另一方面，在绘制世界地图时，需要把整个球面展开到平面上，此时，经度的大圆，作为测地线，甚至比例尺看起来会扭曲的非常奇怪，但其实这正是球面实内禀弯曲这一特性的体现。

如何在弯曲时空上找出某条测地线，并确定它的表达呢。为了解决这一问题，首先要问一个矢量如何在沿线平移途中变化。矢量的各分量一般以逆变形式给出，所以第一步要推导的是逆变张量的协变导数。注意到协变张量和逆变张量之间有通过度规决定的对应关系

将它代入到对协变张量求协变导数的定义（1）式中，再利用相容性条件（2）式，不难推出

求导的结果是一个二阶张量，它给出的是矢量的四个分量在四个不同方向上的十六个斜率。如果给定特定的小平移

矢量的整体变化可以写为

这一式子可以类比于平直时空中的向量平移，同样平移出一段Δr的举例后，一个三维矢量，比如某个力 F 的各分量变化是

在弯曲时空中，这一计算也是类似成立的。

为了衡量变化率，一般要求这一小平移的长度为单位长度，所以要除上任意小平移的长度，它即由线元给出

和狭义相对论中所讨论的一致，三维空间中的线元是距离，四维时空中的线元是时空间距，同也是运动的粒子的原时。于是，除以线元长度后，矢量沿某个方向平移的带来的变化是

其中第一项变成了普通的，可以看成是对原时的求导。而第二项修正中，

可以认为是一个速度项，或者用几何的语言，是时空中某条路径或者说轨迹的切矢量。

上面的讨论中，所取的矢量 U^m 是任意的，不妨将其取到和上述所提的路径的切矢量一致，此时有

张朝阳解释，它对应的是某一路径或者轨迹的切矢量，沿着轨迹做平行移动（parallel transport）时的变化率。在平直时空中，一条直线上各点的切矢量自然是不变的。将其推广，弯曲时空的“直线”应当要满足同样的要求。所以，一条测地线应当满足上述方程等于 0，展开来写，即

再利用切矢量的定义（3），可以得到二阶方程

积分结果就是一条“弯曲时空的直线”，它即是引力作用下测试粒子的运动轨迹。

张朝阳提醒，仔细观察测地线方程，注意到 ds 可以被解释为粒子原时，不难发现它和牛顿第二定律有非常类似的形式。等号右边可以被解释为加速度，它与测试粒子本身的质量无关，只决定于由克氏符描述的时空弯曲的形式。这一结果符合课程开始时的爱因斯坦对弱等效原理的思考结论。这是一种全新的观点来看待万有引力的作用，强调了“引力本质是空间弯曲”这一结论。

（张朝阳推导弯曲时空中的测地线方程）

据了解，《张朝阳的物理课》于每周周五、周日中午12时在搜狐视频直播，网友可以在搜狐视频APP“关注流”中搜索“张朝阳”，观看直播及往期完整视频回放；关注“张朝阳的物理课”账号，查看课程中的“知识点”短视频；此外，还可以在搜狐新闻APP的“搜狐科技”账号上，阅览每期物理课程的详细文章。

cbs sports bettingslot game casino free onlineonline casino free bonus no deposit

---

声明：该文观点仅代表作者本人，搜狐号系信息发布平台，搜狐仅提供信息存储空间服务。